Para sa mga pagkukulay na figure ▽
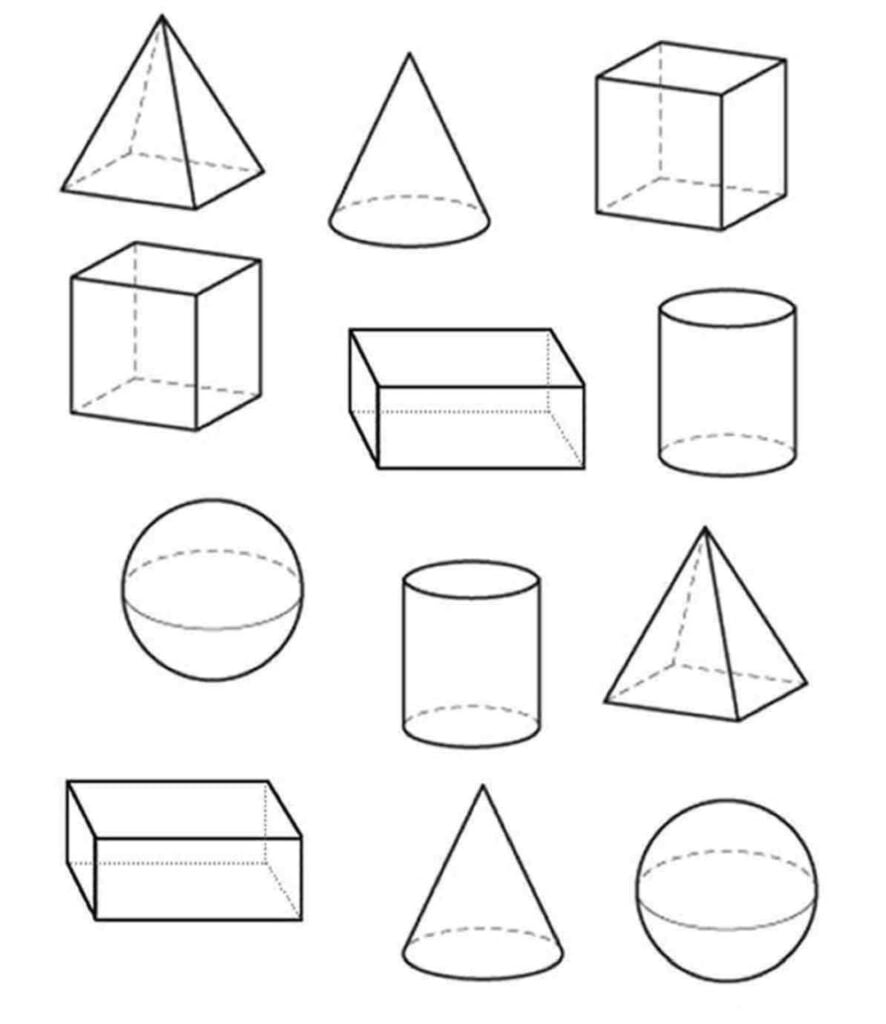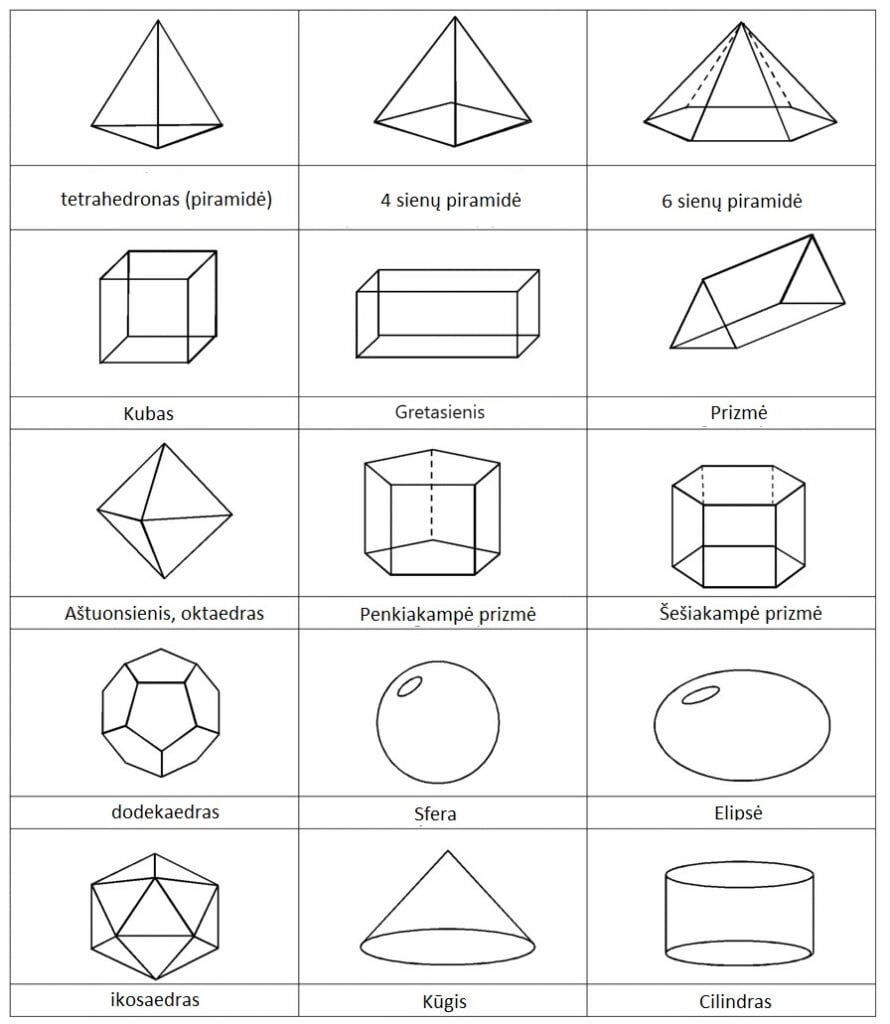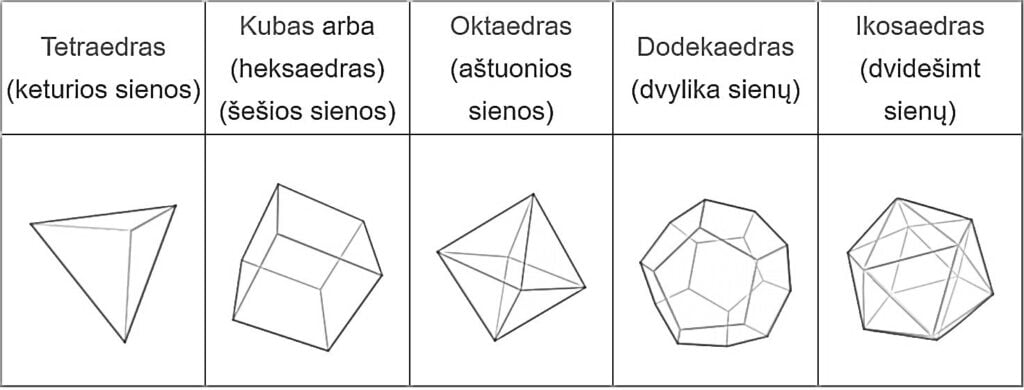
Sa pamamagitan ng pagkulay ng mga geometric na figure, mapapabuti ng mga bata ang kanilang pang-unawa sa pagkukulay at bigyang pansin ang mga pagkakaiba sa mga hugis, bumuo ng kanilang pagkamalikhain at makapagpahinga. Ang mga pagkukulay na figure ay isang mahusay na paraan upang ipahayag ang iyong sarili at ang iyong personalidad, dahil ang bawat pagguhit ay natatangi at indibidwal. Ang geometric figure ay isang hugis o pattern na naglalarawan sa mga geometric na relasyon ng mga bagay sa espasyo, tulad ng isang parihaba, bilog, tatsulok, atbp. Mga form para sa pagkukulay.
Bilog, bilog, bola sa kulay. Ang isang bilog ay espesyal dahil ang lahat ng mga punto nito ay katumbas ng layo mula sa gitna at maaaring ilarawan ng parehong radius. Kung susukatin natin ang lapad nito at i-multiply sa 3.14, malalaman natin ang lapad nito.
Cube, Parihabang paralelogram para sa pangkulay. Ang kubo ay isang three-dimensional na geometric na katawan. Mayroon itong anim na parisukat na mukha. Ang lahat ng mga anggulo nito ay mga tamang anggulo, iyon ay, 90 degrees.
Square, parihaba para sa pangkulay. Ang parisukat ay isang regular na polygon na may pantay na haba ang lahat ng apat na gilid at ang lahat ng anggulo nito ay katumbas ng 90 degrees. Ang lugar ng isang parisukat ay katumbas ng parisukat ng haba ng gilid.
Isang regular, equilateral triangle para sa pangkulay. Ang equilateral triangle ay isang tatsulok na may magkaparehong haba ang lahat ng panig. Ito ang tanging uri ng tatsulok kung saan ang lahat ng mga anggulo ay pantay, sila ay 60 degrees. Ang mga ugat ng mga dahon ng maraming halaman ay nakaayos sa hugis ng isang equilateral triangle.
Rhombus sa kulay. Ang rhombus ay isang may apat na gilid na ang lahat ng panig ay magkapareho ang haba at ang lahat ng magkasalungat na panig ay magkatulad. Ito ay tulad ng isang naka-compress na parisukat, o isang inilatag na parisukat, ngunit tiningnan mula sa gilid. Ang lugar ng isang rhombus ay madaling kalkulahin: Lugar = a * h. Kung saan ang a ay ang haba ng gilid ng rhombus, oh ang taas ng rhombus.
Ellipse para sa pangkulay. Ito ay tulad ng isang patag na bilog. Ito ang trajectory kung saan ang mga planeta ay gumagalaw sa paligid ng araw, bagaman sa katotohanan, ang mga ellipse ng mga planeta ay halos bilog. Ang mga ellipse ay may iba't ibang kapal. Ang isang regular na ellipse ay madaling iguhit, ang kailangan mo lang ay sinulid, isang lapis at dalawang karayom (i-google ito).
Oval para sa pangkulay. Maaari naming tawagan ang isang hugis-itlog na anumang figure na nakakatugon sa mga sumusunod na pamantayan: Ito ay may dalawang axes ng symmetry. Ang haba nito ay mas malaki kaysa sa lapad nito. Ang lapad nito ay higit sa kalahati ng haba nito. Samakatuwid, maaari nating tawagan ang isang hugis-itlog na ellipse, isang itlog, isang olibo, isang raspberry, isang mansanas, isang peras, isang pipino, isang track ng kotse, isang stadium, atbp.
Mga 3D na hugis upang kulayan
Mga 3D na hugis na may mga pangalan: tetrahydron (pyramid), 4- at 6-sided na pyramids, cube, rectangle, prism, octahedron, pentagonal prism, hexagonal prism, dodecahedron, sphere, ellipse, icosahedron, cone, cylinder.
Mga polyhedron, polyhedron
Trapezium para sa pangkulay. Ang trapezoid ay isang quadrilateral na may hindi bababa sa dalawang magkatulad na panig. Ang mga magkatulad na panig na ito, na tinatawag na mga base, ay lumikha ng isang kawili-wiling geometric na bagay kung saan hindi lahat ng panig ay parallel sa isa't isa, ngunit medyo simetriko pa rin.
Cilindras spalvinimui. Cilindras turi du identiškus, lygiagrečius apskritimo formos pagrindus. Jo šoninė paviršiaus dalis yra plokščia ir, jei ji būtų išvystyta, sudarytų stačiakampį. Cilindras yra ašiškai simetriškas - jei jį perpjausime per abu pagrindus, abu gauti pusiau cilindrai bus identiški. Taip pat, cilindras yra simetriškas pagal bet kurią pločio pusrutulį, per jį einančią tiesę, kuri jungia abiejų pagrindų centrinius taškus.
Maraming iba't ibang mga geometric na hugis
Ang mga polygon ay may kulay
Parallelogram, trapezoid, heptagon, octagon, pentagon, hexagon
Mga Figure: Bituin, puso, gasuklay, krus, hemisphere, arrow
Hanapin ang tamang figure
Para sa pagputol ng mga numero
Mga figure na may mga tuldok na linya
Hectagon, heksagono
Polygonal triangle sa pagkukulay
Iba't ibang pigura
gulong ng gear
Ang isang kono (kono) ay isang natatanging geometric na pigura na may isang bilog na base at isang solong tuktok kung saan ang lahat ng mga punto ng base ay kumonekta. Ang dami ng isang kono ay maaaring kalkulahin bilang isang-katlo ng dami ng isang silindro na may parehong base at taas.
Matutong gumuhit ng mga hugis
Pyramid sa kulay. Isang space figure na may isang base na gilid at lahat ng iba pang mga gilid ay nagtatagpo sa isang punto.
Platonic solids: tetrahedron, cube (hexahedron), octahedron, dodecahedron, icosahedron
Ang globo ay ang hanay ng lahat ng mga punto sa espasyo na katumbas ng layo mula sa isang sentral na punto.
Border para sa pangkulay. Ang lahat ng mga anggulo ng isang parapet ay katumbas ng 90 degrees, at ang magkasalungat na mga ibabaw ay pantay at parallel. Ang surface area ay katumbas ng 2(ab+bc+ca), kung saan ang abc ay magkaibang panig. Ang dami ay kinakalkula sa pamamagitan ng pagpaparami ng haba ng magkaibang panig.
Ang tamang tatsulok ay para sa pangkulay. Lugar = (haba ng base * taas) / 2.
Trapezium
Isang bituin sa isang bilog